OHM'S LAW

Probably the most important mathematical relationship between voltage, current and resistance in electricity is something called “Ohm’s Law”. A man named George Ohm published this formula in 1827 based on his experiments with electricity. This formula is used to calculate electrical values so that we can design circuits and use electricity in a useful manner. Ohm's Law is shown below.

OHM'S LAW I = V/R, I = current, V = voltage, and R = resistance *Depending on what you are trying to solve we can rearrange it two other ways. V = I x R R = V/I *All of these variations of Ohm’s Law are mathematically equal to one another.

Let’s look at what Ohm’s Law tells us. In the first version of the formula, I = V/R, Ohm's Law tells us that the electrical current in a circuit can be calculated by dividing the voltage by the resistance. In other words, the current is directly proportional to the voltage and inversely proportional to the resistance. So, an increase in the voltage will increase the current as long as the resistance is held constant. Alternately, if the resistance in a circuit is increased and the voltage does not change, the current will decrease.

The second version of the formula tells us that the voltage can be calculated if the current and the resistance in a circuit are known. It can be seen from the equation that if either the current or the resistance is increased in the circuit (while the other is unchanged), the voltage will also have to increase.

The third version of the formula tells us that we can calculate the resistance in a circuit if the voltage and current are known. If the current is held constant, an increase in voltage will result in an increase in resistance. Alternately, an increase in current while holding the voltage constant will result in a decrease in resistance. It should be noted that Ohm's law holds true for semiconductors, but for a wide variety of materials (such as metals) the resistance is fixed and does not depend on the amount of current or the amount of voltage.

As you can see, voltage, current, and resistance are mathematically, as well as, physically related to each other. We cannot deal with electricity without all three of these properties being considered.

Example of question :

1. A simple electrical circuit consisting of a battery as a power source voltage ε and a load resistor R.

 

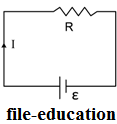
If ε is 12 volts and R is 3 Ω specify:
a) strong current flowing
b) the amount of charge that flows in 1 minute

Solution :
a) strong current flowing
For a simple circuit as above just use:
I = ε / R
I = 12/3
I = 4 A

b) the amount of charge that flows in 1 minute

Q = I x t
A Q = 4 x 60 sec
Q = 240 Coulomb

 

2. A direct current electrical circuit consists of a 12 volt battery, and three resistance, respectively:

R₁ = 40 Ω
R₂ = 60 Ω
R₃ = 6 Ω

Define:
a) The total resistance in the circuit
b) Strong circuit current (I)
c) a strong current in the resistance R1
d) a strong current in the resistance R2
e) whether Itotal, I1 and I2 satisfy Kirchhoff's current law?

  Solution :

a) Rtotal = R1 + R2 + R3
1/Rp = 1/40 = 1/60 = 5/120
Rp = 24
Rtotal = 6Ω + 24Ω = 30Ω
b) Strong circuit current
I = 12 volt / 30 Ω
I = 0.4 A
c) a strong current in the resistance R1
I1 = Itotal x (R2 / (R1 + R2)
I1 = 0.4 x (60 / (40 + 60)
I1 = 0.4 x (60 / (100) = 0.24 A
d) a strong current in the resistance R2 I2 = Itotal x (R1 / (R1 + R2) I2 = 0.4 x (40 / (40 + 60)
I2 = 0.4 x (40 / (100) = 0.16 A
e) whether Itotal, I1 and I2 satisfy Kirchhoff's current law?
According to Kirchhoff's current law,
ΣImasuk = ΣIkeluar
So the number of I1 and I2 be the same as Itotal = 0.4 A
Itotal = I1 + I2
Itotal = 0.24 + 0.16 = 0.40 A, according to the results of the calculation point b above.